The Algorithm Behind Ragas in Carnatic Music

In Carnatic (and in Hindustani, though this blog post will focus on Carnatic) music, there is the concept of raga. At face value, a raga is just a scale or a collection of notes. Think of it as a subset of 16 possible notes:

\[R \subset \{S, R1, R2, R3, G1, G2, G3, M1, M2, P, D1, D2, D3, N1, N2, N3\}.\]

Each of these notes has a name, e.g. $S$ is Shadjam, and the numbers appended to the end of a letter are variations of the note (sharpened or flattened versions of the note). If not counting variations, we have $7$ notes or swaras. As you can see, $S$ and $P$ do not have variations. Each raga also defines an ascending (Arohana) and descending order (Avarohana). Formally, these can be defined as a tuple $A = (S\dots)$ and $V = (SA\dots),$ where $SA$ is $S$ but in the next higher octave.

Note: There are ragas with arohana and avarohanas that are not sorted, e.g. one note is higher than the previous in the avarohana. These ragas that “zig-zag” are called vakra ragas.

Overall, a raga scale can be loosely related to the Western “Do Re Mi…”

Melakarta Ragas

A Melakarta Raga is a raga $R_{M}$ with the following conditions:

1. There are exactly $7$ notes used in the arohana and avarohana, one of each swara
2. The arohana and avorohana are sorted. (This and the above condition make the arohana and avarohana symmetric)
3. The upper $SA$ is included in the scale.

As per this definition, we know that, to construct a Melakarta raga $R_{M},$ we have $1$ choice for $S$, $3$ choices for $R$ ($R1, R2, R3$), etc. Multiply all this out and we get

\[1 \cdot 3 \cdot 3 \cdot 2 \cdot 1 \cdot 3 \cdot 3 = 162\]

possible ragas.

The actual number of Melakartas

But… that’s actually not right. Turns out that $R2$ is the same pitch as $G1$ and $R3$ is the same pitch as $G2$. This means that we actually just have $6$ $R, G$ pairs:

\[\{(R1, G1), (R1, G2), (R1, G3), (R2, G2), (R2, G3), (R3, G3)\}.\]

These pairs, combined with the specification of which $M$ note ($M1$ or $M2$) actually are given a name: chakras. Each of the $2 \cdot 6 = 12$ chakras has a name as well: “Indu”, “Netra”, “Agni”, “Veda”, “Bana”, “Ritu”, “Rishi”, “Vasu”, “Brahma”, “Disi”, “Rudra”, “Adi”.

Similarly, due to analogous equality in pitches, we have $6$ $D, N$ pairs:

\[\{(D1,N1),(D1,N2),(D1,N3),(D2,N2),(D2,N3),(D3,N3)\}.\]

Now, if we multiply all our options, we get:

\[S \cdot (\text{6 $R, G$ pairs}) \cdot (M1, M2) \cdot P \cdot (\text{6 $D, N$ pairs})\] \[= 1 \cdot 6 \cdot 2 \cdot 6 = 72.\]

Therefore, there are $72$ Melakarta ragas.

Explore these Melakartas yourself

Click on a raga name and a sidebar will open. You can click on the buttons to play the notes and also view the graph below to visualize the relative distance between the notes.

Melakarta Numbers

Each melakarta is assigned a number, defined by the algorithm below:

    
\begin{algorithm}
\caption{Notes from Raga Number $n$}
\begin{algorithmic}
\PROCEDURE{notation}{$n$}
    \STATE $R, G, M, D, N$ \COMMENT{these will store the kind of swara (note), e.g. R = R1}
    \IF{$n > 36$}
        \STATE $M = M1$
        \STATE $n \leftarrow n - 36$ 
    \ENDIF
    \STATE chakra = $\lceil \frac{n}{6} \rceil$
    \STATE let $f: \{1\dots6\} \rightarrow \{(R1, G1), (R1, G2)\dots\}$, where $f$ maps to the corresponding $R, G$ pairing for a given chakra number (implemented as a list, with input being index)
    \STATE $R, G = f(\text{chakra})$
    \STATE subNumber = $(n - 1) \mod 6 + 1$
    \STATE let $g: \{1\dots6\} \rightarrow \{(D1, N1), (D1, N2)\dots\}$, analogous to $f$
    \STATE $D, N = f(\text{subNumber})$
    \STATE return $R, G, M, D, N$ \COMMENT{not returning S or P as they come in only one form}
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}

Note: Here the chakra number is between 1 through 6, as in this definition, I did not include $M$ notes as part of the specification.

This algorithm yields the ordering below (image from Wikimedia)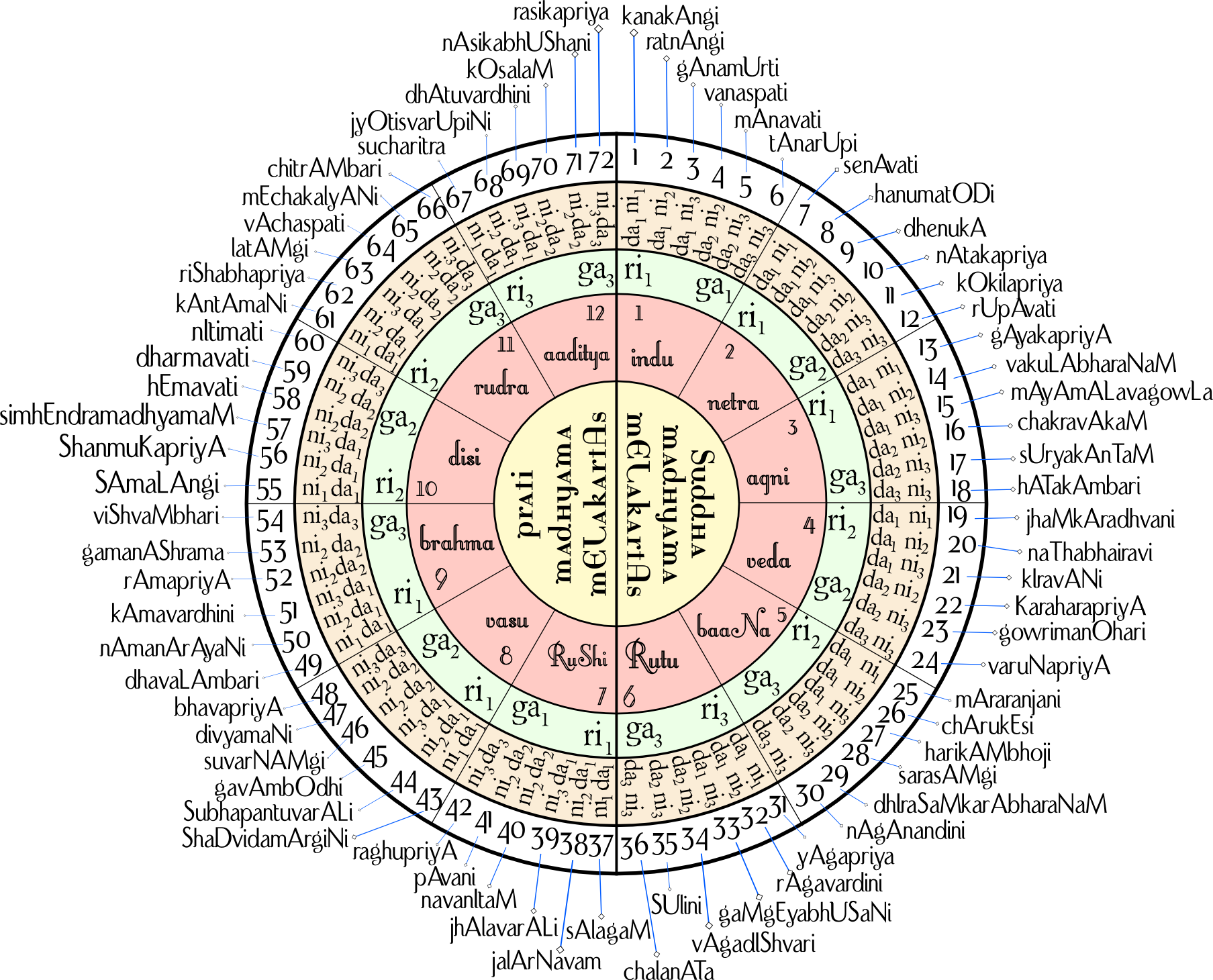

One other awesome property of this system is that the first two syllables of the names of melakartas correspond to their numbers. This means that by knowing just the name of the raga, you can deduce the notes that comprise it! This is done through the Katapayadi system, where syllables are assigned digits. As an example, for the raga Dheerasankarabharanam, dha corresponds to $9$ and ra corresponds to $2$. Therefore, the raga number is $29$. You can read more about this here.

Fun Fact: The ragam Dheerasankarabharanam was originally Sankarabharanam, whose name was changed to fit this system.

There is so much more to this

So far, we have just been talking about the notes that comprise a raga. However, as I said, that is just taking a raga at face value. A raga specifies gamakams or transitions between notes, emotions that are conveyed through the notes, and so much more.

There are also janya ragas which are subsets of melakartas, which are a world of their own! A cool resource that will teach you more about them can be found here: ragaoftheweek.com.

This system of ragas is what allows musicians in Carnatic music to structure their notes. Some benefits of this include being able to do improvisations that still match with the composition (as they stick to the same raga).

I hope to make more blog posts on this topic and encourage you to explore this music theory even more!